[Originally published as A Modern Version of an Ancient Spherical Earth Experiment]
Most people who were unfortunate enough to receive a public education think that ancient people believed the earth was flat. Indeed, I thought this myself until I started studying the history of science. If you do the same, you will learn that the earth was known to be spherical even in ancient times.
In fact, the shape of the earth was so obvious to ancient Greek scholars that when Archimedes mathematically derived his Law of Buoyancy in roughly 250 BC, this was his second postulate:
The surface of any fluid at rest is the surface of a sphere whose centre is the same as that of the earth.
In other words, bodies of water are spherical because the earth is spherical. This was necessary for him to demonstrate what causes objects to float or sink.
Because the spherical shape of the earth was so well-known among ancient Greek scholars, Eratosthenes decided to measure the distance around the sphere in roughly 240 BC.
He heard that there was a city called Syene in Egypt in which the sun was directly overhead at midday on the summer solstice. He traveled to Syene to make sure this was correct.
On that date, he waited for the sun to reach its highest point in the sky and then looked down a deep well. He saw that its sides cast no shadow onto the water at the bottom of the well. This told him the sun was directly overhead. If there had been a pole sticking straight out of the ground, it would not have cast a shadow.
The next year, he traveled to a city called Alexandria. When the sun reached its highest point in the sky on the same date, he measured the length of the shadow of a pole that was sticking straight up out of the ground. With the height of the pole, the length of its shadow, and the distance between Syene and Alexandria, he determined the circumference of the earth.
This brings me to the topic of this post.

A YouTube personality, Scimandan, decided to get his listeners to help him do a modern version of the experiment.
Essentially, he told them to wait until the sun was highest in the sky on the Northern Hemisphere’s summer solstice and do what Eratosthenes did — measure the length of the shadow cast by a vertical object. The image above shows me doing this with a level. I sent him my latitude and longitude, the height of the level, and the length of its shadow, as did 1,013 others from all over the world (both hemispheres). He compiled the results and shows them in this video.
He displays three graphs that clearly show the earth is a globe.
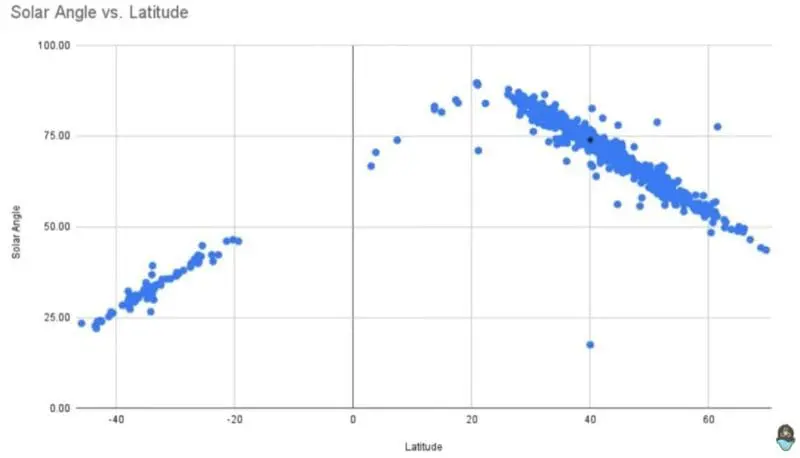
First, he uses trigonometry to calculate the sun’s angle of elevation for each person’s result and then graphs that based on the person’s latitude. The black dot shows where my data point is on the graph:
He then shows what the results should look like for both a spherical earth and a flat earth:
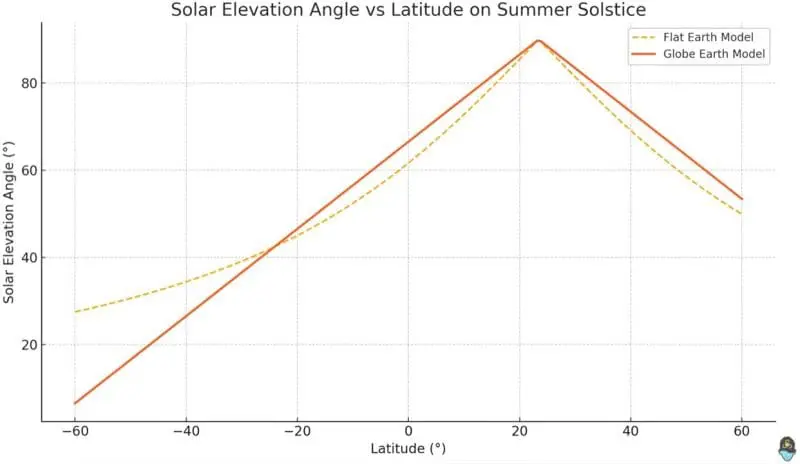
As you can see, aside from a few outliers, the data correspond to what you expect for a spherical earth, and not what you expect for a flat earth. More importantly, he calculates the ratio of the shadow length to the object’s height for all the results, and graphs them according to latitude. Once again, the black dot shows where my data point is on the graph.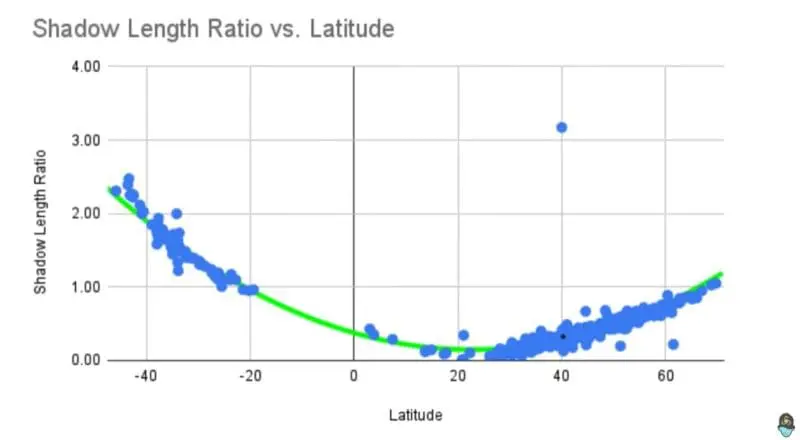
The green curve is what you expect for a spherical earth, while a flat earth should show a linear relationship. Obviously, the data are only consistent with a spherical earth.
Near the end of the video, he chooses three data points that occur roughly along the same longitude. He then uses those points to do what Eratosthenes did: calculate the distance around the sphere. Those three data points give a value that is within 4% of the known circumference of the earth.
As this crowd-sourced experiment shows, you don’t have to rely on modern technology or photos from space to understand the shape of the earth. Ancient Greek scholars could figure out that it was spherical because careful observations on earth demonstrate it.







