[Originally published as Mathematics and Science]
Was mathematics discovered or invented?
This might seem like an odd question, but it is an important one. I haven’t seen any official poll on the matter, but I suspect that most mathematicians, philosophers, and scientists would say that it must have been invented. After all, math is a tool. We use it for accounting, parceling out land, etc. Surely people invented this tool and then improved on it over time. If that’s really true, however, there is a deep mystery that is awfully hard to explain. Nobel laureate Dr. Eugene Wigner (a theoretical physicist and mathematician) put it this way:
The first point is that the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it.
Think about it. We didn’t invent the natural world. We simply study it. If we invented mathematics, why does it play such an integral role in our understanding of the natural world?
In my opinion, there is no mystery as to why mathematics is so useful in the natural sciences. That’s because I don’t think we invented it; I think we discovered it. Indeed, I think it is the language of creation. As Galileo wrote:
[The universe] cannot be read until we have learnt the language and become familiar with the characters in which it is written. It is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word.
I was reminded of Galileo’s wise words when I read a short paper by two professors from my alma mater, the University of Rochester.
The paper discusses using a quantum mechanical technique known as variational computation to determine the energy levels in an atom. The quantum mechanical model is (so far) the most accurate model of the atom. However, the mathematics are very complex. As a result, the equations cannot be solved in an exact manner for most atoms. That’s where variational computation comes in. It allows you to approximate the solutions for the equations so that you can apply the quantum mechanical model to any atom. The more approximations you make with variational computation, the more precise your solutions become.
In mathematics, there are also things that must be approximated.
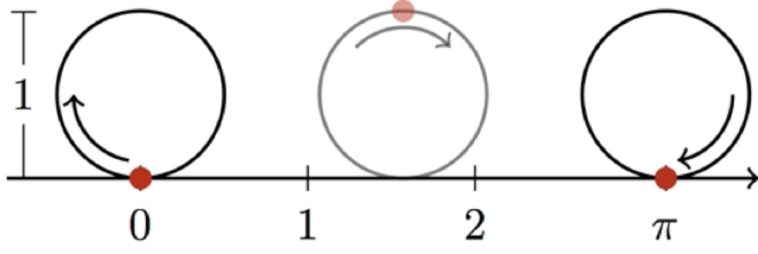
One of them is the value for pi, the ratio of the distance around a circle to the diameter of that circle. The drawing at the top of this post gives you a way to visualize what pi means. If a wheel has a diameter of 1 meter, it will travel a distance of pi meters when it makes one complete rotation without slipping. It turns out that the value of pi cannot be calculated in an exact manner. Instead, its value must be approximated.
- If you do a few approximations, you get 3.14.
- If you do a few more, you get 3.1416.
- If you do a few more, you get 3.14159.
The more approximations you do, the more accurate decimal places you will get, and therefore, the more precise your value for pi will become. However, you will never get an exact value for pi, because there isn’t one. The decimal places go on forever. Because of that, pi is called an irrational number.
How does this relate to the paper I am discussing?
Well, the authors decided to apply variational computation to a system that doesn’t require it: the hydrogen atom. This atom is simple enough that the equations of the quantum mechanical model can be solved exactly, so there is no need to approximate their solutions. Nevertheless, the authors decided to approximate the solutions anyway. When they did, they noticed something. Their solution ended up containing an equation that had been developed by a natural philosopher named John Wallis back in 1655, more than 200 years before quantum mechanics was proposed!
Back then, Wallis developed one of the means by which mathematicians can approximate the value of pi. It turns out that this same approximation simply “falls out” of quantum mechanics when variational computation is applied to the hydrogen atom. In other words, the physics of the hydrogen atom contains one of the means by which we determine pi! As the authors state:
The existence of such a derivation indicates that there are striking connections between well-established physics and pure mathematics that are remarkably beautiful yet still to be discovered.
Indeed. Modern science is still demonstrating the truth of what Galileo wrote nearly 400 years ago.