[Originally published as the first part of Infinity]
Infinity is the concept of an unlimited quantity. Although this idea is challenging for us, it is very real because it stems from the mind of God. God’s understanding is infinite (Psalms 147:5). Therefore, to study the nature of infinity is to learn something about the nature of God.
The Logic of Numbers
How can finite minds such as ours possibly know anything about the infinite? How can we reason about a concept that goes beyond our finite ability to conceive? The answer to both questions is revelation. God has revealed some of His thoughts to us. Therefore, we can know about some things that go far beyond our ability to fully grasp.
Eternity is one manifestation of infinity — an infinite amount of time.
The Bible teaches that those who have received Christ as Savior and Lord by grace through faith will enjoy eternal life with God (John 3:15-16, 4:14, 5:24, 6:40,47, 10:28). Although we cannot fully grasp the implications of eternity, we have some concept of it because God has placed this concept in our heart — in the core of our being (Ecclesiastes 3:11). We, therefore, have an awareness of a concept that we cannot fully grasp.
Only the biblical worldview can make sense of this.
But how can we reason properly about a subject that we cannot fully comprehend? The answer again is found in revelation. God has gifted us with the tools of logic and mathematics. Logic is the principles of correct reasoning. These principles stem from the mind of God, and we have access to them because we are made in God’s image. We can use the principles of logic even in areas that go beyond our ability to fully understand.
Mathematics is simply the logic of numbers. We can use mathematics to draw true conclusions about numbers — even when such numbers are infinitely beyond our ability to comprehend! Mathematics is therefore a divine gift that allows us to know truths that our minds cannot fully contain.
The Different Sizes of Infinity
Using the tools of logic that God has gifted to us, we can learn things about infinity that are often counterintuitive to our finite mind. For example, mathematicians have discovered that some types of infinity are “bigger” than other types of infinity. Furthermore, sometimes two sets of infinite numbers are exactly the same size, even if one contains all the numbers of the other set and more! One example of this concerns the counting numbers.
The counting numbers are all the positive integers: 1,2,3,4, and so on.
They are infinite in extent because the positive integers never end; you can always add 1 and get the next positive integer. So, the set of all positive integers is infinite. Now consider the set of all integers (both positive and negative, as well as zero). Clearly, the set of all integers is infinite because it is unlimited in both the positive and negative directions.
Our intuition suggests that the set of all integers is a larger set than the set of only the positive integers. After all, the set of all integers contains all the positive integers, all negative integers and zero. Since one set entirely contains the other as well as numbers that are not in the other, it would have to be bigger, right?
But our intuition is wrong.
In fact, the set of all integers is exactly the same size as the set of only the positive integers. Both sets are infinite and they are the same infinity.
But how do we know this? One way to show that two sets of numbers are exactly the same size is to show that for every number in one set, there is exactly one number in the other set.
For example, the set containing only 1,2,3, and 4 is the same size as the set containing only 5,6,7, and 8. For each number in the first set there is exactly one number in the second set. One way to show this is to add 4 to each number in the first set and we will have a corresponding number in the second set. That is, 1 corresponds to 5, 2 to 6, 3 to 7, and 4 to 8.
Since each number in the first set can be linked to exactly one number in the second set, the two sets are the same size. Using this same method, we can show that each number in the set of all integers matches exactly one number in the set of positive integers.

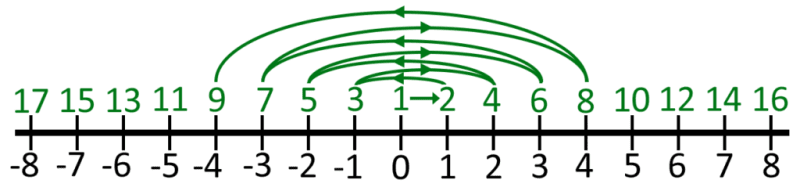
Imagine the set of all integers as displayed on the number line.
Starting with zero, we place a number 1 above it.
Then we go right to number 1 and place a 2 above it as shown in the figure above.
Then we move to negative 1 and place a 3 above it.
Then we go to positive 2 and place a 4 above it.
Then we go to -2, 3, -3, 4, -4, and so on,each time writing the next positive integer just above the number as illustrated in the figure below.
We can see that for each number in the set of all integers, there is a corresponding positive integer (written just above it). We can do this forever in principle without ever running out of numbers. Clearly, for each integer, there is a corresponding positive integer. Therefore, the set of all positive integers is exactly the same size as the set of all integers! Both sets are infinite, and they are exactly the same infinity.
This is deeply counterintuitive because one set completely contains all the numbers in the other and then some. Yet, the two sets are the same size.
This would not be possible for finite sets.
But infinity often yields surprising results.
To be continued…







