[Originally published as Algebra, Giraffes, and God’s Handiwork]
The following is adapted from the new Algebra 2 program we’re writing; check out the store for other math curriculum that will help math come alive for your students.
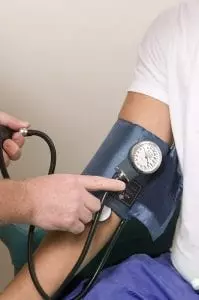
Ready for a glimpse of God’s handiwork as we apply algebra out of a textbook? Well, here we go! We’re going to look at how blood pressure relates to the distance from the heart.
First off, here’s a basic definition of blood pressure from Blood Pressure UK:
“When your heart beats, it pumps blood round your body to give it the energy and oxygen it needs. As the blood moves, it pushes against the sides of the blood vessels. The strength of this pushing is your blood pressure.”[1]
Have you ever noticed that when a nurse takes your blood pressure, they always do it on the top part of your arm? That’s because “[m]edical personnel are trained to measure blood pressure at heart level.”[2] The top of your arm is at the same level as your heart. This is important, as, because of gravity, the pressure changes throughout the body.
If a person’s blood pressure equaled a specific amount at heart level (which we’ll call P0), then the pressure at another part of the body (which we’ll represent with a P) could be approximately found by this formula, where h is the distance from the heart:
Blood pressure at another part of the body = Blood pressure at the heart + (density of the blood)(acceleration on the blood due to gravity)(height or distance from the heart)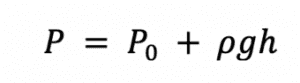
To better understand this, know that if you were to take your blood pressure on your feet while standing, it would be higher than if you were to take the pressure on your arm. That makes sense, as gravity is pulling blood downwards, creating more pressure on your feet.
This also means that if you were to elevate your feet and take your blood pressure there, there’d be less pressure. BUT your heart would have to work harder to overcome gravity to get blood to your feet.
Stop and bend over for a second. You get a head rush, don’t you? That’s because of the extra blood pressure as your head gets lower.
Now think of a giraffe. Its head is waaaay above its heart. Does its heart have to pump extra to get blood there? And when it bends down to drink, how much pressure does its head have to be able to handle?
While there’s more to blood pressure than just the distance from the heart, we can temporarily ignore those other factors and just look at the change in pressure between what it would be at the heart and what it is at a different location. In the formula above, we used P0 to stand for the blood pressure at the heart. Let’s remove that and just look at the change in the pressure from the blood pressure at the heart.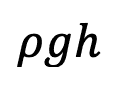
We’ll also assume that the acceleration due to gravity and density stay the same: 9.807 m/s2(which is the approximate gravity on earth), and an approximate density of blood (ρ) of 1,060 kg/m3. If we substitute these values in for ρ and g, we get this: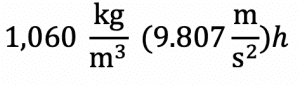
Depending on what value we plug in for our height (h), we’ll get a different value. The product will show us the change in pressure from the heart due to the change in height.
Let’s start by looking at a human. The top of my head is about 0.508 meters above my heart (about 20 inches). What would the approximate blood pressure be due to the distance from my heart when I bend down and touch my head to the floor? To find that, I’ll replace the h in the formula with 0.508 meters.![]()
We wrote the answer in both metric units and mmHg, which is the same units you’ve probably heard your blood pressure given at the doctor’s office when you go for a checkup. Normal blood pressure runs between 80 to 120 mmHg, so it makes sense that the change in pressure would be around 39.610 mmHg which is on the same order of magnitude with normal blood pressures but still less than the average.
In comparison, what would a giraffe’s blood pressure be at the top of its head due to the distance from the heart when it bends down for a drink if it’s head was 6 ft (1.829 m) above[3] its heart? We’ll plug 1.829 m into the same formula.![]()
Notice that the change in pressure due to the distance from the heart is 142.611 mmHg versus only 39.610 mmHg for a human. That is more than 3.5 times as much!
When they bend, giraffes have a much higher blood pressure rushing to their heads due to their larger size! If God had not specially designed the giraffe to handle this pressure, giraffes would have died out from all the blood rushing to their head went they bend down. In a 2017 article published on the Answers in Genesis website[4], Karin Viet explains what a testimony to God’s design giraffe’s are:
Evolutionists also encounter a design dilemma for the evolution of a long neck. That six-foot neck requires an intricate blood vessel system to maintain proper blood pressure between the heart and brain. A giraffe bending its neck down to drink water is a marvelous display of design. The 25-pound heart that pumps blood way up that neck against gravity suddenly pumps down with gravity, which should cause the delicate brain to explode. But the blood vessels are uniquely designed with reinforced walls, bypass valves, a cushioning web, and sensor signals to moderate the pressure when the giraffe bends its neck down.
The reverse of this intricate system happens when the giraffe raises its head so that the pressure is regained and the giraffe doesn’t pass out. In addition, the tight skin on giraffe legs has been compared to an astronaut’s G-suit, because it prevents high blood pressure from pressing blood out of the capillaries.
 Giraffes were given just what they need—G-suit and all—to be able to handle the higher pressure caused by their long necks. And it’s math (including algebra!) that helps us understand how giraffes are a marvel of God’s grand design![5]
Giraffes were given just what they need—G-suit and all—to be able to handle the higher pressure caused by their long necks. And it’s math (including algebra!) that helps us understand how giraffes are a marvel of God’s grand design![5]
Don’t let your students miss out on seeing how math helps us explore God’s handiwork.
Footnotes
[1] “What is blood pressure?” Blood Pressure UK, (England, 2008), http://www.bloodpressureuk.org/BloodPressureandyou/Thebasics/Bloodpressure, s.v., “Blood Pressure.”
[2] Based on physics.wm.edu/~labs/107_manual/ch11.pdf
[3] Based on a neck of 6 ft, as shared by the San Diego Zoo https://animals.sandiegozoo.org/animals/giraffe and the fact that its heart is located in the giraffe’s chest.
[4] https://answersingenesis.org/mammals/giraffes-towering-testimonies-to-gods-design/
[5]See also https://bpsfuelforthought.wordpress.com/2012/08/14/why-giraffes-dont-have-brain-damage/ for more details.








Evolutionists When they see these signs, they immediately ask about the recurrent laryngeal nerve .
What is the true answer?