Overview
The circle is such a common shape that we rarely give it any significant thought. The undeniable truth is, however, that no matter how hard we try it is utterly impossible to either find a perfect circle in nature, or to construct a perfect circle by any physical means.
In fact, without the concept of ∞ (infinity) it would be utterly impossible even to theorize the notion of a perfect circle.
A true circle can never be the result of construction or calculation; but, is in reality a concept that we must reason out from the relationship between measurable and immeasurable ‘values’.
The Not-so-well-rounded Truth
There are three reasons why perfect circles cannot exist in our physical universe:
- Common – Those objects which appear to be nearly circular to our unaided eye will always either resolve themselves into degenerate shapes (such as ovals), or reveal line or arc segments not harmonious with the remainder of the circumference.
- Constructed – At some point even the most carefully constructed circle breaks down in its radius, however infinitesimally, and fails to be a perfect circle.
- Calculated – Since the one value upon which every circle is dependent, π, is itself an ‘unknown’ value, we cannot with absolute accuracy calculate all of the values necessary to define a circle with perfect precision.
The ‘common’ and ‘constructed’ circles as described above are examples of physical objects. It would be fair to say that based on the criteria given in these descriptions no object would truly meet the requirements of its ‘perfect’ shape at all levels. At some point when we examine the shape of any object at the molecular, atomic, or subatomic level, we will eventually find imperfections that render definition of any ‘perfectly-shaped’ object pointless. This is especially true when we consider that many subatomic particles are traveling and/or vibrating and incredible rates, making exact measurements of all particles at any ‘exact’ point in time utterly futile.
Therefore, while circles (and therefore arcs – which are circle segments, cones, and spheres – which are three-dimensional compositions of circles) fail the physical test of perfection, so do all other shapes based on those same criteria.
For this reason we will confine our examination of the circle to the criteria listed under the third reason listed above – that of the ‘calculated’ circle.
How to ‘Reason Out’ a Circle
Unlike shapes which have all straight sides, exact values of all components of a circle can never be determined. This is because the relationship between the curved surface (known as the circumference) and its base dimension (called the diameter) is a transcendental value which we call π. While we can estimate the value of π to an astounding number of decimal places (usually far more than we would ever need for everyday calculations) we can never know its exact value.
The value π (pi) is among the many values representing real mathematical relationships in our physical world. Such constant values are known as irrational numbers because their exact value cannot be calculated. This is also true of many numbers like ⅓ which as a decimal becomes 0.333333…. However, unlike the value of ⅓, which can be represented by an exact numerical or mathematical expression, π cannot be represented in the same manner – but only approximated. This kind of number is called a transcendental number1.
In order to ‘reason out’ a circle, let’s begin with the simplest regular polygon – an equilateral triangle.
A regular polygon is a polygon having all sides of equal length and all included angles of equal value.
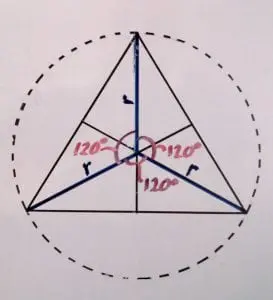
By constructing a line from each corner of the triangle (solid black) to the midpoint of each opposite side, then locating the intersection of these lines, we can find the center of triangle as shown in figure 1. Notice the circumscribed circle (dashed black) in this figure. The center of the triangle and the center of the circle occupy the same point. Therefore the radius of the circle is the same length as any one of the three line segments (blue) from the corner of the triangle to the center of the triangle. We will call this the triangle radius (r).
In figure 1 we also see that the hub angle (red – also called the ‘central angle’) between each radius line is 120°. This value is determined by dividing the number of degrees in a circle (360) by the number of sides in the triangle:
360°/3 sides = 120° hub angle
As the number of sides of any regular polygon increases, the number of hub angles increases; and conversely, the value of each hub angle subsequently decreases.
To illustrate this principle, let’s look at a square, which is a four-sided regular polygon.
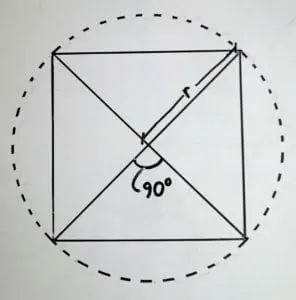
Notice in figure 2 that the center of the square is found by drawing lines from each corner to the opposite corner and locating the intersection. Again the center of the square is at the same location as the center of the circumscribed circle.
From this we learn that locating the center of a regular polygon is dependent upon the number of sides it has. For regular polygons with an even number of sides connect any two opposite corners to find the center. For regular polygons with an odd number of sides connect any two corners with the midpoints of the opposite sides.
Notice this time that the hub angle is smaller because there are more sides to the polygon.
360°/4 sides = 90° hub angle
This relationship will continue to be true as the number of sides in the polygon increases:
360°/5 sides = 72° hub angle
360°/6 sides = 60° hub angle
360°/10 sides = 36° hub angle
360°/100 sides = 3.6° hub angle
Using this method we can approximate the shape of a circle with a regular polygon having so many sides that it appears to be round. This process is illustrated in figure 3 below.
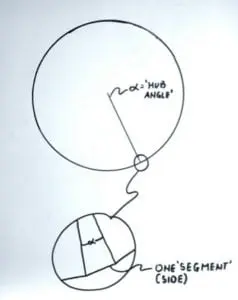
This figure ‘represents’ a regular polygon that has 10,000 sides. At the scale shown it has the ‘appearance’ of being a circle; however, if we look at the magnified section shown in the lower portion of the figure we see that this shape is, in fact, comprised of many tiny segments connected at very shallow angles to one another. The two ‘radius’ lines drawn from the polygon center to its corners form such a narrow angle that at this scale they appear to be a single line. To determine the value of this tiny hub angle we simply use the previously established relationship:
360°/10,000 sides = 0.036° hub angle
We can write an expression for this relationship for any regular polygon as follows:
Single hub angle = 360°/n; n = # of sides
As we can readily see, a circle can be very closely approximated mathematically and graphically by constructing regular polygons of with ever-increasing numbers of sides. However, the problem of representing a ‘perfect circle’ is that the perimeter (circumference) of the circle is defined as a smooth arc2 drawn 360° about a center point at a distance (r) defined as its radius.
A smooth arc has no line segments along its surface, but is made up entirely of points3. As we shall see in a moment, those points must have a length of ‘zero’ (0) in order for the arc to be perfectly smooth. This is where the impossibility of even the mathematical representation of a circle begins.
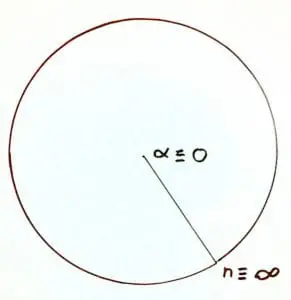
Figure 4 is a simple representation of the basic requirements for a ‘perfect circle’ based on the regular polygon side-angle relationship we have been looking at in this article. In this diagram the Greek letter ‘α’ (alpha) represents the hub angle and ‘n’ represents the number of sides in the polygon. The only way for the circumference to become perfectly smooth is for all of the segments to become so tiny that there is no longer any angle left between them at all. The only way that this is possible is if the length of each side shrinks to the point that it has no length at all!!!
Of course when the length of a side of the polygon becomes zero then there can be no distance between the endpoints of the radius lines forming the hub angle. Therefore, the hub angle (α) then also becomes 0 (zero).
To represent this ‘absolute’ condition mathematically we write:
For a perfect circle to exist α ≡ 0
Since we know from our previously established side-angle relationship that:
Single hub angle = 360°/n; n = # of sides
or rewritten as:
α = 360°/n
then:
n = 360°/α = ∞
Since in a ‘perfect circle’ α ≡ 0, then n ≡ ∞
The ‘impossibility’ problem arises here when we try to ‘absolutely’ equate infinity to the number of ‘sides’ in a circle. This is because infinity is not an actual value, but a concept of an ever-increasing quantity. So while we can reason and comprehend the ‘concept’ of a perfect circle, we can never truly represent one either graphically or mathematically.
This is one of the many ways in which the Lord has placed His Signature upon His Creation. He has actually built concepts and ideas into our physical universe that we can only truly represent through intuition because no finite value exists by which we can define them. Yet, these concepts are real, useful, and even necessary for our existence in everyday life. Such is the case with the humble circle. We all know and clearly understand what a circle is; but, beyond an intuitive definition there is no method by which we can exactly represent one either graphically or mathematically.
While we can reason and comprehend the ‘concept’ of a perfect circle, we can never truly represent one either graphically or mathematically.
The Infinite and the Eternal
The Lord in His infinite wisdom has designed an incredibly simple shape which we call a ‘circle’ with an ‘impossible’ definition. This shape not only demonstrates the infinite genius of our Creator; but, it also bears several traits in common with Him as well. For this reason I consider the humble circle one of the many ‘signatures’ of the Hand of God upon His Creation.
Like the Lord God, a perfect circle has ‘no beginning’ and ‘no ending’. In Revelation 1:8 we read the words of the glorified Lord Jesus as He speaks to the Apostle John and states, “I am Alpha and Omega, the beginning and the ending, saith the Lord, which is, and which was, and which is to come, the Almighty.” He repeats this statement three (3) more times in Revelation. The literal translation of the first portion of this passage is: ‘I am the Α (Alpha) and the Ω (Omega), beginning and ending…’
The above passage from Revelation also reiterates the Eternal nature of God in the phrases: “which is” (present), “and which was” (past), “and which is to come” (future). Furthermore, this passage also links the Omnipresent Nature of God to the Omnipotent (“the Almighty”) Nature of God. This makes perfect sense because God, being of an infinite nature, is infinitely powerful. Therefore, anything in our universe that points to infinity must, by definition, point to our Creator. Thus ‘infinity’ becomes the ‘Signature’ of God.
In Psalm 139:7-8 the psalmist writes, “Whither shall I go from thy spirit? or whither shall I flee from thy presence? If I ascend up into heaven, thou art there: if I make my bed in hell, behold, thou art there.”
From the references in Revelation we know that God is Eternal – existing at ‘all times’. From the passage above out of Psalm 139 we know that He is in ‘all places’. From these passages we then conclude that the Lord God exists in the ‘Eternal Now’ – everywhere at all times. This is illustrated in the ‘perfect circle’ which has no breaks or gaps, but covers a continuous path at all time in all directions with no beginning or ending.
Summary
In Revelation 13:8 we read of the “Lamb slain from the foundation (literally ‘founding’) of the world”. Simply put, before God ever created our world (and therefore, mankind upon the word) He had already perfected His plan of redemption for fallen mankind. The ‘Lamb’ – Christ Jesus – had already been slain for our sins long before the man Jesus ever took that dreaded walk to Calvary to be nailed to a cross in fulfillment of Isaiah chapter 53. In God’s perfect Omniscience He knew not only what mankind would do in sinning against Him after Creation; but, He also knew what sacrifice would be necessary to be offered up in order to provide the free gift of redemption to all who would come to Him by faith (Ephesians 2:8-9).
“…behold, now is the accepted time; behold, now is the day of salvation.”
-2 Corinthians 2:6
“For whosoever shall call upon the name of the Lord shall be saved.”
-Romans 10:13
In His Love,
Dr. Jack L. Burton
-Hebrews 11:1-3
References
(1) Math Open Reference. Regular Polygon.
http://www.mathopenref.com/polygonregular.html
(2) Merriam-Webster Dictionary. Infinity.
http://www.merriam-webster.com/dictionary/infinity
Additional Reading
(1) Infinity – The Signature of God. Dr Jack L. Burton.
(2) A Brief History of π.
http://www.math.com/tables/constants/pi.htm
(3) The History of Infinity – G. Donald Allen, Texas A&M University. [PDF]
End Notes
1. Infinity – The Signature of God. Dr Jack L. Burton.
2. Math Open Reference. Arc.
http://www.mathopenref.com/arc.html
3. Math Open Reference. Point.
http://www.mathopenref.com/point.html
Notes
1. All Bible quotes in this article are taken from the KJV.
2. Bible passages in double quotes (“) appear exactly as found in the KJV.
3. Bible passages in single quotes (‘) have been modified for emphasis or ease of reading only (such as capitalization of pronouns referring to God, bolded text, or modernized punctuation, etc.) without altering the actual wording of the text.
Disclaimer: While to the author’s knowledge all of the information cited in the referenced material related directly to the content of this article is correct and accurate, the author in no way endorses any of the cited references in their entirety – especially where the material contained therein is in direct contradiction with the Creation account given in the Word of God.








The pupil of the eye?
James,
That is a great observation!!!
Not only is the human eye in general an incredible example of God’s design in His creation of mankind; but, the pupil itself is one of the ‘gates’ mentioned in Scripture by which the outside world enters into the ‘mind’. This would make a great message as well.
In His Love,
Dr. Jack L. Burton
-Hebrews 11:1-3